
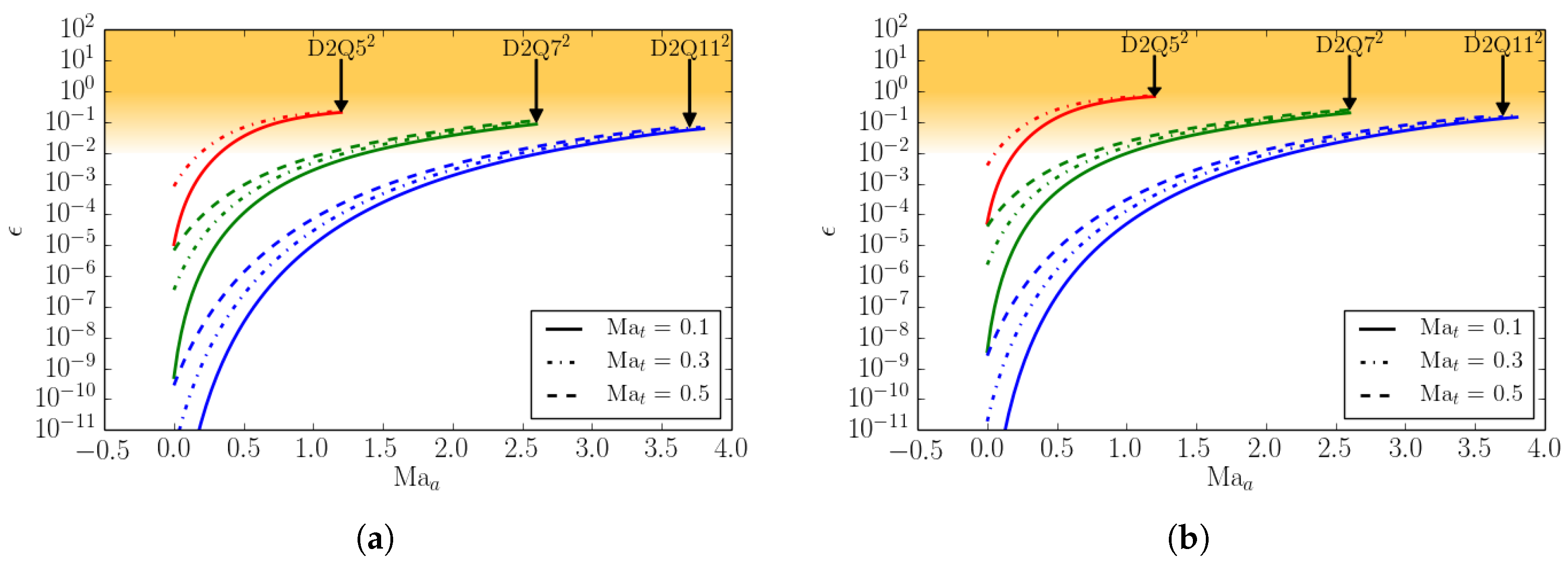
The link arises via probability, as the total number of arrangements is much larger than the number of arrangements that conform to a certain order principle. Boltzmann entropy, named after the Austrian physicist Ludwig Boltzmann, is a fundamental concept in statistical mechanics that quantifies the level of. Results In the review, two classes of methods were identified. The consistency of different computational methods was investigated. The original concept of entropy was first introduced by the German theoretical physicist Rudolf Clausius into thermodynamics in 1865. The term and the concept are used in diverse fields, from classical thermodynamics, where it was first recognized, to the microscopic description of nature in statistical physics, and. In that sense, loss of order is loss of information and increase of disorder is an increase in entropy. A systematic survey of the efforts to compute the Boltzmann entropy of a landscape was performed. Entropy is a scientific concept, as well as a measurable physical property, that is most commonly associated with a state of disorder, randomness, or uncertainty. We can further associate order with information, as any ordered arrangement of objects contains information on how they are ordered. The equilibrium state is the macrostate that lacks most information on the underlying microstate. begingroup user115350 right, im trying to show that the statistical (Boltzmann) entropy and thermodynamic entropy are the same (and Im most interested in a very general proof of this equality, one which isnt restricted to specific systems like ideal gases or something). Lewis: "Gain in entropy always means loss of information, and nothing more". It follows, what was stated before Shannon by G. The concept applies to non-equilibrium states as well as to equilibrium states. The more microstates are consistent with the observed macrostate, the larger is this number of questions and the larger are Shannon and Gibbs entropy.
We note that this is exactly the type of experiment presumed in the second Penrose postulate (Section ). When expressed with the binary logarithm, this amount of Shannon information specifies the number of yes/no questions that would have to be answered to specify the microstate.

kB is the Boltzmann constant, and fhost fhostLP fhostNP. It is the amount of Shannon information that is required to specify the microstate of the system if the macrostate is known. in the internal energy and entropy of the host caused by the structural transition.


 0 kommentar(er)
0 kommentar(er)
